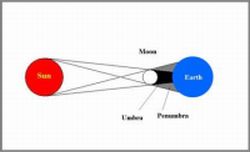
A solar eclipse occurs when the Moon passes precisely between the Earth and the Sun and its shadow falls on Earth and moves over it. The Earth, Moon and Sun are then aligned when viewed from above the orbital plane of the Earth or from the side.
Fig (1)
The geometry of solar eclipses
The orbit of the Moon is not exactly circular; it is rather slightly elliptical in shape, with the Earth located at one of the foci of this orbit. So, the Moon's distance from the Earth changes along its orbit from a minimum value of about 363,300 km to nearly 406,000 km .
(The minimum and maximum distances of the Moon from the Earth are termed perigee, and apogee respectively. These terms are of Greek origin.)
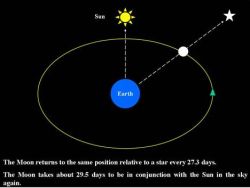
The Moon orbits the Earth every 27.32 days. This period is known as the sidereal period of the Moon as it is measured relative to the stars. That is, in this period, the Moon completes one orbit around the Earth and returns to the same position relative to the stars in the sky. As the stars are so distant from the Earth, their intrinsic motions are negligible when compared to the Moon's orbital motion, and the stars are assumed fixed with respect to the Moon.
As the Moon orbits the Earth, it returns to the same position relative to the Sun in the sky every about 29.53 days or 709 hours. This is the synodic period of the Moon, on which the months of the lunar calendars (e.g. the Islamic calendar) are based.
Unlike the stars, the Sun appears to move across the sky, and cannot be considered stationary relative to the Moon. This apparent solar motion is due to the orbital motion of the Earth around the Sun. Since the Earth revolves around the Sun, the Sun is actually stationary relative to the Earth, but from our point of view we feel that the Sun orbits the Earth and moves around the sky every year.
This is similar to the apparent motion of trees relative to a passenger on a train.
During the synodic period, the Moon goes through a complete cycle of phases from New Moon through waxing crescent, First Quarter, waxing gibbous, Full Moon, waning gibbous, Last Quarter, and waning crescent to New Moon back again.
Fig (2)
The luner phases
Fig (3)
The sidereal and synodic periods of the Moon
Likewise, a lunar eclipse happens when the Earth, Sun and Moon are aligned and the Moon passes in the shadow of the Earth.
This happens at Full Moon.
Frequency
If the orbit of the Moon were in the plane of Earth's orbit around the Sun, there would be a solar eclipse every New Moon and a lunar eclipse every Full Moon, but this is not the case. From any spot on Earth we see a total eclipse of the Moon about every 2 years and a partial solar eclipse less frequently.
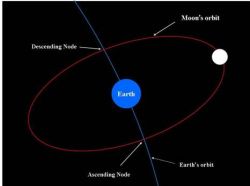
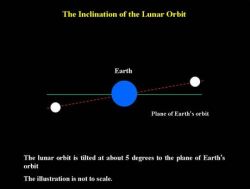
This is due to the tilting of the lunar orbit at a small angle of about 5 degrees to the orbital plane of the Earth, which is also known as the ecliptic. The orbit of the Moon intersects the Earth's orbital plane at two points known as the nodes. The two nodes are known as the ascending node and the descending node, respectively.
Fig (4)
The ascending and descending nodes of the luner orbit
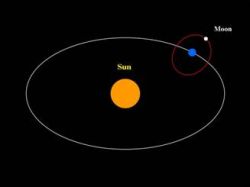
The lunar orbit is tilted at 5 degrees to the orbital plane of the Earth.
There are two points of intersection between the two orbital planes termed the ascending and descending nodes.
When the Moon crosses the ascending node, it moves north of the ecliptic and when it crosses the descending node it moves south of the ecliptic.
Fig (5)
The inclination of the luner orbit
To have a solar eclipse, the New Moon must be near or at a node. For a total or annular eclipse to occur, the Moon must pass precisely through a node.
Astronomical computations show that the New Moon can be at most 18.5 degrees from a node to cause a partial solar eclipse.
The Moon crosses the two nodes every month as it orbits the Earth. Usually, the New Moon passes above or below a node, but every 6 months the New Moon actually verifies the solar eclipse condition, and a solar eclipse occurs somewhere on Earth. Therefore, we have at least two solar eclipses every year.
Over 2,500 years ago, through their painstaking, accurate observations of the sky, the Babylonian astronomers discovered that approximately every 18 years, 10 days, and 8 hours (6585 1/3 days), the Earth, Moon and Sun return to approximately the same positions relative to each other. This period is known as the saros and it is applicable to lunar eclipses as well.
If a solar eclipse occurred on a given date, then after one saros another solar eclipse of almost the same circumstances will occur. Since the saros period is not an exact integer number of days, i.e., it is 6585 + 1/3 days long, the Earth will have rotated 120 degrees through this 1/3 of day (one-third of a complete rotation about the Earth's axis), and consequently, the eclipse path will be shifted westwards and the eclipse will not be visible for most of the locations that witnessed the first eclipse.
For example, there was a total eclipse of the Sun on 11 August 1999 visible across Europe , and there will be another solar eclipse on 21 August 2017. The latter eclipse will be visible across North America , i.e., it will not be visible in most of the locations it traversed on 11 August 1999.
Map (1)
The path of the 11 August 1999 total solar eclipse
Map (2)
The path of the 21 August 2017 solar eclipse
It is obvious, however, that after three consecutive saros periods, or approximately 54 years, 31 days, the solar eclipse will return to the same geographic region. This period is known as the triple saros. However the eclipse will not be necessarily total in the same locations.
For instance, the eclipse of 11 August 1999 was partial in Egypt, and actually, there will be a total solar eclipse on 12 September 2053 (after three successive saros periods). This eclipse will not be total in Europe again. The totality path of that eclipse will toy pass Europe, but, fortunately, it will cross the Nile Valley in Upper Egypt.
Map (3)
The path of the total solar eclipse of 12 September 2053
Astronomical computations showed that a solar eclipse will not recur at intervals of one saros forever. A series of saros periods contains up to 87 solar eclipses, and is only about 1,226 to 1,550 years long.
Ancient astronomers in Mesopotamia and Greece were able to predict solar eclipses in the first millennium BEC. Now, modern astronomers, through their elaborate studies of the motions of the Moon and the Earth, can predict the dates and paths of future solar and lunar eclipses with an amazing accuracy. |

